GRoT> - Graficzny Rozwiązywacz Tarcz

P1: Kwadratowa płyta z otworem

Rozciąganie płaskiej, kwadratowej płyty z otworem służy jako częsty przykład obliczeniowy dla wykorzystania teorii płaskiego stanu naprężeń. Model obliczeniowy jako mapa bitowa zapisany jest w katalogu programu w projects/plate.bmp. Przejdźmy bez zwłoki do rozwiązania tego problemu w programie GRoT>

1. Utworzenie geometrii modelu

Płyta jest stalową blachą kwadratową o boku długości 200 mm, średnicy otworu 80 mm i grubości 4 mm. Do jednego jej boku przyłożona jest siła rozciągająca równa 1000 N. Drugi bok utwierdzony jest w osi kierunku rozciągania, a dwa węzły środkowe tego boku utwierdzone są w obu kierunkach. Materiałem płyty jest stal o module sprężystości równym 210 GPa oraz liczbie Poissona 0,3. Model obliczeniowy przygotowany w Paincie przedstawiony jest poniżej.

1.2. Oznaczenia kolorów powyższego modelu

Cyjan - elementy skończone modelu tworzące kwadrat o boku 50 pikseli
Biały - wycięcie otworu o średnicy 20 pikseli
Czerwony - utwierdzenie węzłów w kierunku poziomym
Niebieski - utwierdzenie węzłów w obu kierunkach
Fioletowy - nadanie siły w kierunku poziomym o wartości 5000 N

Tak utworzona mapa bitowa jest następnie zapisana w katalogu programu grot w folderze projects jako plate.bmp

2. Przygotowanie pliku wejściowego

Gotowy plik wejściowy dla tej analizy można pobrać z niniejszego adresu tutaj. Musi on zostać umieszczony pod nazwą input.txt w katalogu programu GRoT>.

Najważniejsze komendy w pliku wejściowym dla problemu rozciąganej płyty są następujące. Ustawienie rodzaju analizy jako płaski stan naprężeń, wskazanie nazwy pliku geometrii, przypisanie materiału, przeskalowanie modelu czterokrotnie (bok wyrażony w pikselach to 50, w rzeczywistości jest to 200 mm) i nadanie siły dla koloru fioletowego. Jest to realizowane przez poniższe polecenia.

problem planestress bmp grot.bmp mat steel scale 4 load x 1000 y 0 magenta

Pozostałe polecenia opisane są w pełnym pliku wejściowym, który jest dostępny domyślnie w katalogu programu lub można pobrać go przez odnośnik na początku tego rozdziału.

3. Uruchomienie analizy

Rozpoczęcie obliczeń odbywa się poprzez wywołanie skryptu Python. Może to zostać zrealizowane w wierszu poleceń systemu Windows, w terminalu systemu Linux lub inny znany użytkownikowi sposób. Poniższa instrukcja dotyczy urochomienia programu dla systemu Windows w wierszu poleceń cmd.exe. W tym wypadku folder programu GRoT> umieszczony jest w podanym katalogu: C:\grot\

cd C:\grot\ python run.py

3.1. Wyjście programu

Jeśli cały proces przebiegł pomyślnie to w konsoli powinna zostać wyświetlona poniższa informacja jako krótki raport z przebiegu obliczeń.

GRoT> ver. 1.0.0, [Graficzny Rozwiązywacz Tarcz] ................................................ Bitmap to finite elements model translation [100.0 %] Created [2377] nodes Created [2236] elements Prepared boundaries applied to eles: [red : 48] [blue : 2] [magenta : 50] Blue boundary [fixed support] applied to [6] nodes Red boundary [in x-dir support] applied to [100] nodes Property of all eles set to [steel] (205.0 GPa, 0.3) Unit system changed to [mm] Standard nodal dimension set to [4.0 mm] Thickness of all eles set to [1.0 mm] Applied force vector (1.0e+03 N, 0.0e+00 N) distributed to [102] nodes Building global stiffnes matrix [100.0 %] Built [4754 x 4754] matrix Storing reserved [316.4] Mbytes of memory Solving... (this may take a while) Succesfully and directly solved system of linear equations Calculated strain and stress tensors (reduced 1-point integration)

4. Uzyskane rezultaty

Pliki graficzne rozwiązania dostępne są w folderze results/plate/. Analityczne rozwiązanie tego zagadnienia wskazuje, że w płycie wystąpią naprężenia średnie równe 8,3 MPa, a maksymalne na krawędzi otworu w płycie równe 18,3 MPa. Przyjrzyjmy się wynikom analizy.

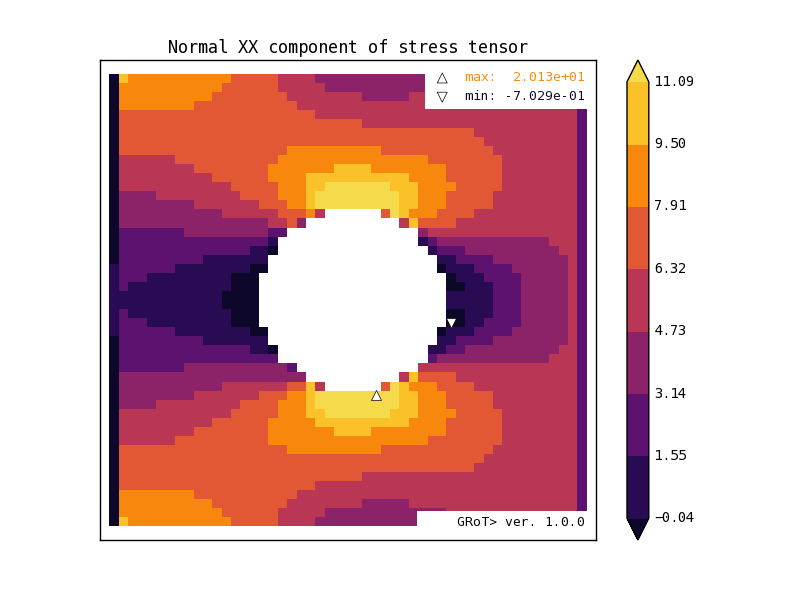
Maksymalne naprężenia normalne uśrednione do elementu w kierunku poziomym uzyskane w analizie równe są 20,1 MPa. Miejsce ich występowania na modelu zaznaczone jest trójkątem obróconym do góry. Skala wyników dobierana jest tak, by środkowa wartość wyników dla wszystkich elementów była w połowie skali, natomiast wartość maksymalna i minimalna oddalone są od niej o 3 odchylenia standardowe. W porównaniu z wynikiem rozwiązania analitycznego analiza wypada całkiem dobrze mając na uwadzę małą liczbę elementów, wśród których wszystkie są kwadratowe i tym samym nie mogą wiernie oddać kształtu wyciętego otworu.